(1.9)  The Chromatic Scale

There is a magic number in western music, known as the twelfth root of two, and it has a value of approximately 1.0595.  This is the number that, when multiplied by itself twelve times, gives a result of two.

Why is this important to music?

Remember that with notes one octave apart, the higher note has double the frequency of the lower note.  The range of frequencies in between is divided up into the twelve steps that give us all of our notes.

The frequency of a note, when multiplied by the twelfth root of two, gives the frequency of the next note up.  The difference in pitch between adjacent notes is called a semitone.

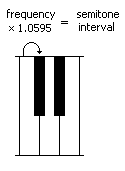
After doing this for twelve notes, you end up with twice the frequency, which is the note one octave up from the starting note.  We can do this in both directions (multiplying upwards and dividing downwards) to calculate the frequency of every musical note.

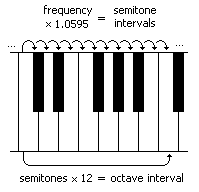
The set of all musical notes is called the Chromatic Scale, a name which comes from the Greek word chrôma, meaning color.  In this sense, chromatic scale means 'notes of all colors'.  Colors, in fact, are also made up from different frequencies, those of light waves.

Because notes repeat in each octave, the term 'chromatic scale' is often used for just the twelve notes of an octave.

This method of dividing the octave using the twelfth root of two is known as equal temperament tuning, pioneered several centuries ago in the time of JS Bach.  Since then, the music of the western world has been based on the notes of the Chromatic scale.

Equal temperament tuning was a major breakthrough in the development of music.  It replaced the earlier method of using simple frequency ratios to divide up the octave, which had great limitations when trying to transpose music from one key to another (more on what this means later).